C03_Intro : Outils mathématiques pour la mécanique du solide

Cours

défilement haut

Outils vectoriels >
Outils torsoriels v
- Définition
- Propriétés et opérations sur les torseurs
- Eléments centraux d'un torseur
- Torseurs particuliers

défilement bas

Masquer le plan

Afficher le plan

Eléments centraux d'un torseur

On suppose que le torseur 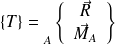est entièrement connu.

Point central

Définition :

Un point central est un point où le moment est colinéaire à la résultante :

$\boxed{\text{ C point central de } \{ T \} \Leftrightarrow \vec M_C = \lambda \, \vec R \,}$

Axe central

Définition :

On appelle axe central d'un torseur le lieu géométrique des points centraux. On montre que ce lieu est une droite telle que :

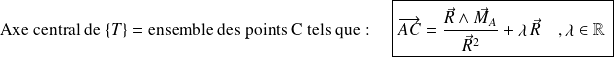
$\text{Axe central de } \{T\} \text{ = ensemble des points C tels que : } \quad \boxed{\overrightarrow{AC} = \frac { \vec R \wedge \vec M_A} {\vec R ^2} + \lambda \, \vec R \quad ,\lambda \in \mathbb{R} \,}$

Remarque :

En pratique, pour déterminer l'axe central : on calcule les coordonnées d'un point C pour une valeur particulière de 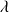( 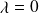en général). L'axe central est la droite passant par le point C et de vecteur directeur .

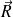Complément : Démonstration

Soit 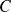un point central de 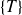. Par définition,

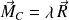
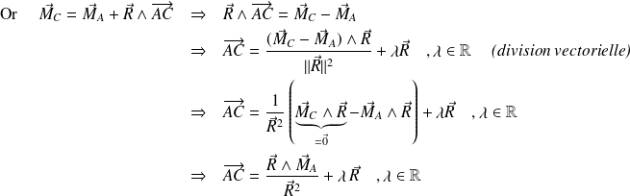
$\begin{eqnarray*} \text{ Or } \quad \vec M_C= \vec M_A + \vec R \wedge \overrightarrow{AC} & \Rightarrow & \vec R \wedge \overrightarrow{AC} = \vec M_C- \vec M_A \\ & \Rightarrow & \overrightarrow{AC} = \frac {(\vec M_C- \vec M_A) \wedge \vec R} {\Vert \vec R \Vert ^2} +\lambda \vec R \quad ,\lambda \in \mathbb{R} \quad \textit{ (division vectorielle)}\\ & \Rightarrow & \overrightarrow{AC} = \frac 1 {\vec R^2} \left( \underbrace{\vec M_C \wedge \vec R}_{=\vec 0 } -\vec M_A\wedge \vec R\right)+\lambda \vec R \quad ,\lambda \in \mathbb{R}\\ & \Rightarrow & \overrightarrow{AC} = \frac { \vec R \wedge \vec M_A} {\vec R ^2} + \lambda \, \vec R \quad ,\lambda \in \mathbb{R} \end{eqnarray*}$

Moment central

Définition :

Il s'agit du moment d'un torseur exprimé en un point central :

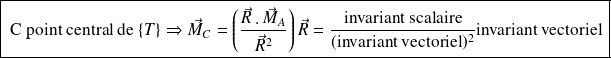
$\boxed{\text{ C point central de } \{ T \} \Rightarrow \vec M_C = \left ( \frac { \vec R \, . \,\vec M_A} {\vec R ^2} \right ) \vec R= \frac{\text{invariant scalaire}} {(\text{invariant vectoriel})^2} \text{invariant vectoriel} \,}$

Complément : Démonstration

Soit 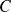un point central de 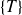. Par définition de l'axe central,

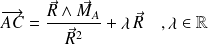
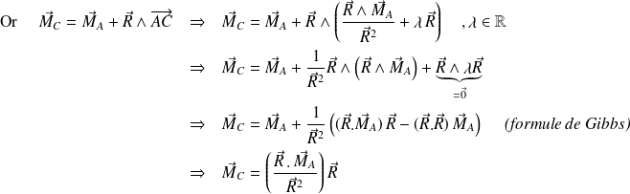
$\begin{eqnarray*} \text{ Or } \quad \vec M_C= \vec M_A + \vec R \wedge \overrightarrow{AC} & \Rightarrow & \vec M_C= \vec M_A + \vec R \wedge \left( \frac { \vec R \wedge \vec M_A} {\vec R ^2} + \lambda \, \vec R \right) \quad ,\lambda \in \mathbb{R} \\ & \Rightarrow & \vec M_C= \vec M_A + \frac 1 {\vec R^2}\vec R \wedge \left( \vec R \wedge \vec M_A \right) + \underbrace{\vec R \wedge \lambda \vec R }_{=\vec 0} \\ & \Rightarrow & \vec M_C= \vec M_A + \frac 1 {\vec R^2} \left( (\vec R . \vec M_A)\, \vec R - (\vec R . \vec R)\, \vec M_A\right) \quad \textit{ (formule de Gibbs)} \\ & \Rightarrow & \vec M_C= \left ( \frac { \vec R \, . \,\vec M_A} {\vec R ^2} \right ) \vec R \end{eqnarray*}$

Propriétés des éléments centraux

Egalité des moments centraux : le moment central est identique en tout point de l'axe central.

Norme minimale : la norme du moment d'un torseur est minimale sur l'axe central. Autrement dit, la norme du moment central est la valeur minimale que peut prendre la norme du moment d'un torseur :

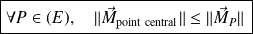
Conséquence : si le moment d'un torseur est nul en un point, alors ce point se trouve nécessairement sur l'axe central et l'invariant scalaire est également nul. Un tel torseur est appelé torseur à résultante ou glisseur.

Forme canonique : Mettre un torseur sous forme canonique signifie le réduire en un point central, donc là où le moment est minimal.

Accueil

Imprimer